Cónicas, parte IV
 |
Autores: Laura Spivak y Pablo J. Kaczor
Responsable disciplinar: Sebastián Vera
Área disciplinar: Matemática
Temática: Cónicas
Nivel: Secundario, ciclo orientado (escuelas técnicas)
Secuencia didáctica elaborada por Educ.ar
|
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia se abordarán los siguientes aspectos: las cónicas como lugar geométrico y el uso de la aplicación GeoGebra como herramienta.
Objetivos de las actividades
Promover la discusión y el intercambio de diversas estrategias entre pares.
Promover el trabajo colaborativo, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Objetivos pedagógicos
Actividad 1: Trazado de la parábola a partir de su directriz y su foco
1) Abran la aplicación GeoGebra y realicen los siguientes pasos para trazar una parábola a partir de su directriz y su foco:
a) Tracen una recta cualquiera, que será la directriz de la parábola, y luego un punto que no le pertenezca, que será el foco. Nómbrenlos de esa manera.
b) Como la distancia de cada punto de la parábola a la directriz se mide con una perpendicular, marquen un punto P en la directriz, y tracen una perpendicular a ella que pase por P. Ese punto P se puede mover a lo largo de la directriz (pruébenlo).
c) Ahora van a buscar un punto de modo que al moverse deje la traza de una parábola. Para pertenecer a ella, ya saben cuáles son las dos condiciones que debe reunir ese punto: estar a igual distancia del foco y de P, sea cual fuere la ubicación de P en la directriz; por lo tanto, ¿en qué recta estará el punto en cuestión? Discútanlo y tracen esa recta.
d) Marquen el punto de intersección entre la recta que trazaron en el ítem anterior y la perpendicular a la directriz. LlámenloC.
e) Muevan P. ¿Cuál es el punto que describe una parábola al moverse? Compruébenlo haciendo que muestre su rastro.
f) ¿Qué sucede si cambian de lugar el foco? ¿Y si cambian la posición de la directriz? Pruébenlo.
g) Guarden la construcción añadiendo una breve síntesis de los pasos que siguieron para hacerla.
Actividad 2: Trazado de la elipse como lugar geométrico
1) Sigan estos pasos con la aplicación GeoGebra para trazar una elipse entendida como lugar geométrico.
2) Decidan cuál será la longitud del eje de la elipse que contiene los focos; marquen con un punto A uno de sus extremos y con la herramienta 
tracen un segmento de esa longitud (por ejemplo, 8 cm). De esa manera, podrán mover el extremo A, pero el eje conservará la longitud que establecieron.
3) Ubiquen uno de los focos en algún punto del segmento y llámenlo F. El otro foco es el simétrico de F con respecto al punto medio del segmento; entonces, para ubicarlo, obtengan el punto medio del segmento con la herramienta 
, y luego el simétrico de F con la herramienta 
. Así habrá quedado marcado F’.
4) Sabemos que la elipse es el lugar geométrico de los puntos cuya suma de distancias a los focos es constante. Esto significa que, en el ejemplo con el eje de 8 cm, si un punto está a 3 cm de F, para pertenecer a la elipse, debe estar a 8 cm - 3 cm = 5 cm de F’; en cambio, si está a 6 cm de F, debe estar a 2 cm de F’, y así con cada uno.
En el primer caso, para ubicar un punto que esté a 3 cm de F y a 5 cm de F’, basta con buscar la intersección de dos circunferencias, como se ve a continuación:
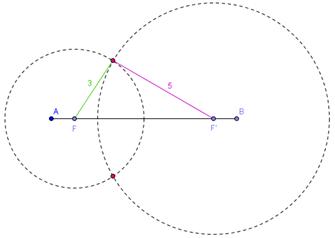
Los dos puntos rojos cumplen la condición, y por lo tanto pertenecen a la elipse que se quiere trazar.
Entonces, hay que conseguir trazar dos radios cuya suma sea constante (en el ejemplo, sus longitudes tienen que sumar siempre 8 cm) y que se puedan modificar al moverse. En GeoGebra eso se consigue usando la herramienta deslizador 
. Esta herramienta permite modificar el valor de un número.
Coloquen un deslizador llamado R1 y, para seguir con el ejemplo, hagan que varíe de 0 a 8 (o de 0 al valor que hayan tomado como longitud del eje). Ese será el radio de una de las circunferencias.
5) Tracen una circunferencia con centro en F y radio R1. Observen cómo varía su radio al mover el punto del deslizador.
6) Ahora, tracen la otra circunferencia con centro en F’. Para que se cumpla que la suma de los dos radios sea 8, el radio de esta debe ser 8 - R1.
7) Marquen la intersección de ambas circunferencias y hagan que los dos puntos, donde se cortan, muestren el rastro.
8) Muevan el punto del deslizador y observen: ¿se va trazando la elipse? ¿Qué pasa si cambian la posición de F? ¿Y si modifican la inclinación del eje que contiene los focos? (Para “embellecer” la construcción, pueden hacer que solo sean visibles los focos y los radios, y si lo prefieren, pueden hacer que junto a cada radio se vea su medida).
9) Hagan las modificaciones necesarias para que la longitud del eje que contiene los focos sea el doble y forme un ángulo de 45º con respecto a la horizontal.
10) Guarden la construcción añadiendo una breve síntesis de los pasos que siguieron para hacerla.
Actividad 3: Trazado de la hipérbola como lugar geométrico
1) Realicen estos pasos con la aplicación GeoGebra, para trazar una hipérbola entendida como lugar geométrico.
2) Marquen dos puntos –que serán los focos de la hipérbola– y llámenlos F y F’.
3) Sabemos que la hipérbola es el lugar geométrico de los puntos, cuya diferencia de distancias a los focos es constante. Decidan cuál será esa diferencia (por ejemplo, 2 cm). Esto significa que, en el caso de tomar 2 cm como diferencia, si un punto está a 5 cm de F, para pertenecer a la hipérbola, su distancia a F’ debe ser 5 cm - 2 cm = 3 cm; o bien 5 cm + 2 cm = 7 cm, como muestra la primera imagen. En cambio, si un punto de la hipérbola está a 6 cm de F, debe encontrarse a 4 cm o a 8 cm de F’ (como se ve en la segunda imagen), y así con los demás.
Los puntos verdes pertenecen a la hipérbola que se quiere trazar, uno a cada rama en cada caso.
Se puede trabajar de manera similar a como se hizo para trazar la elipse, pero con tres circunferencias en juego, como muestra esta imagen referida al primer ejemplo de los dos de arriba:
Esta vez, ya que las ramas de la hipérbola continúan en forma indefinida, en lugar de utilizar un deslizador, se usará una semirrecta con un punto que se mueva libremente sobre ella simulando un “deslizador”. Dibujen una semirrecta auxiliar y llamen O a su origen. Marquen un nuevo punto (Z) sobre ella (prueben que ese punto se puede deslizar libremente sobre la semirrecta).
4) Utilicen la herramienta que se muestra abajo para tomar la distancia desde O hasta Z.
5) Tracen una circunferencia con centro en F y radio distancia OZ. Observen cómo varía su radio al mover el punto Z.
6) Tracen una circunferencia con centro en F’ y radio distancia OZ + 2, y otra de radio distancia OZ - 2 (si es que tomaron 2 cm como diferencia; en el caso contrario, sumen y resten a la distancia OZ el valor que asignaron). Marquen las intersecciones de la primera circunferencia con cada una de las otras dos, pinten los 4 puntos con verde y activen su rastro.
8) Hagan las modificaciones que sean necesarias para que los focos estén sobre una vertical a 20 cm uno del otro, y de modo que la diferencia entre las distancias de un punto cualquiera de la hipérbola a los focos sea de 3 cm.
9) Guarden la construcción añadiendo una breve síntesis de los pasos que siguieron para hacerla.
Actividad 4: Las envolventes
Realicen estos pasos con la aplicación GeoGebra para investigar envolventes de familias de rectas.
Averigüen cuál es el lugar geométrico de las mediatrices de un segmento en los siguientes casos:
1) Cuando uno de sus extremos (P) se mueve sobre una recta.
Para ello, tracen una recta, marquen un nuevo punto P en ella (prueben que P se pueda mover sobre la recta), marquen otro punto C que no pertenezca a la recta, tracen el segmento PC y su mediatriz, activen el rastro de la mediatriz y muevan el punto P. ¿Qué cónica se genera?
2) Cuando uno de sus extremos: P, se mueve sobre una circunferencia.
Para ello, tracen una circunferencia, marquen un nuevo punto P en ella (prueben que P se puede mover sobre la circunferencia), marquen otro punto C que sea interior a la circunferencia, tracen el segmento PC y su mediatriz, activen el rastro de la mediatriz y muevan el punto P. ¿Qué cónica se genera?
Modifiquen la ubicación del punto C de modo que sea exterior a la circunferencia y muevan el punto P. ¿Qué cónica se genera ahora?
3) Repitan los pasos 1 y 2 cambiando la mediatriz por una perpendicular al segmento en el punto P, y estudien los resultados.
4) Guarden los archivos de GeoGebra, peguen todas las imágenes con las respuestas en un archivo de algún procesador de textos y agreguen un análisis de los resultados obtenidos.
Bibliografía / Webgrafía recomendada
Webs interactivas de matemática
Otros ejemplos para observar y analizar (Ver Tangencial)